- http://www.numericana.com/answer/calendar.htm#moon
- (2002-12-28) Hegira Calendar [AH = Anno Hegirae]
The Islamic calendar is called Hijri (or Hijrah calendar).
- The origin of the Muslim calendar is "1 Muharram 1 AH"
(i.e., Friday, July 16, 622 CE)
and predates by a few weeks the
"flight from Mecca"
(Hijra, Latin: Hegira) which,
according to Muslim tradition, took place in September 622 CE.
The numbering of years from the date of the Hegira was introduced in AD 639
(17 AH) by the second Caliph, 'Umar ibn Al-KHaTTab (592-644).
The monthly Islamic calendar itself had already been in use since AD 631
(10 AH) as the Quran prescribes a lunar calendar
without embolismic months (9:36-37).
Before 10 AH, a long forgotten "Arabian calendar" was probably used,
which was similar to the Jewish calendar and had
an intercalary month, now and then, in order
to compensate for the steady drift of the lunar cycle with respect to the solar seasons.
Since an Islamic year (12 lunar months)
falls shorts of a tropical year by almost 11 days,
the Islamic calendar isn't related to the seasons.
Muslim festivals simply drift backwards and return
roughly to the same seasonal point after a period of 33 Islamic years
(which is about a week longer than 32 tropical years).
Traditionally, the beginning of a new Islamic month
is defined locally from the time when the thin crescent
of the young moon actually becomes visible again at dusk,
a day or so after the new moon.
If the moon can't be observed for any reason,
the new month is said to begin 30 days after the last one did.
Tabular Islamic Calendars :
Printed Islamic calendars are most commonly based on
standard arithmetic predictions of moon sightings.
We present the most common of
8 extant variants.
Such schemes were devised by Muslim asronomers
after the eighth century CE. Historians use this routinely to convert an
Islamic date to a Gregorian one (unless a knowledge of
the day of the week allows a precise synchronization with the relevant
local observational calendar).
A regular cycle of 30 years is used, which includes 19 years of 354 days and 11 years of
355 days (modulo 30, the long years are:
2, 5, 7, 10, 13, 16, 18, 21, 24, 26, and 29).
The average Islamic month is thus equal to 29.53055555... days,
which is about 2.9 s shorter than the actual mean synodic lunar month
of 29.530588853 days
(it takes about 2428 tropical years to build up a discrepancy of a whole day).
The standard Islamic year is tabulated below:
| Number | Month Name | Days |
| 1 | MuHarram | 30 |
|---|
| 2 | Safar | 29 |
|---|
| 3 | Raby' al-awal | 30 |
|---|
| 4 | Raby' al-THaany | 29 |
|---|
| 5 | Jumaada al-awal | 30 |
|---|
| 6 | Jumaada al-THaany | 29 |
|---|
| 7 | Rajab | 30 |
|---|
| 8 | SHa'baan | 29 |
|---|
| 9 | RamaDHaan | 30 |
|---|
| 10 | SHawwal | 29 |
|---|
| 11 | Thw al-Qi'dah | 30 |
|---|
| 12 | Thw al-Hijjah | 29 or 30 |
|---|
| |
30 Islamic years
(10631 days)
| 0 | 10 | 20 |
|---|
| 1 | 11 | 21 |
|---|
| 2 | 12 | 22 |
|---|
| 3 | 13 | 23 |
|---|
| 4 | 14 | 24 |
|---|
| 5 | 15 | 25 |
|---|
| 6 | 16 | 26 |
|---|
| 7 | 17 | 27 |
|---|
| 8 | 18 | 28 |
|---|
| 9 | 19 | 29 |
|---|
| 
|
Important Islamic Celebrations
| Date | Arabic | English |
| 10 MuHarram | Ashura |
Remembrance of Muharram |
| 12 Raby' al-awal | Maulidun-Nabi |
Birth of the Prophet |
| 27 Rajab | Laylatul-Mi'raj |
Night of Ascension |
| 15 SHa'baan | Laylatul-Bara'ah
(Shabi-Baraat) |
Night of Record |
| 1 RamaDHaan | RamaDHaan |
Fast of Ramadan (first day) |
| 27 RamaDHaan | Laylatul-Qadr |
Night of Power |
| 1 SHawwal | Eid al-Fitar |
Breaking of the Fast |
| 10 Thw al-Hijjah |
Eid al-Adha |
Sacrifice Festival [3½ days] |
Hijri Calendrical Formulas : (2007-06-22)
The average Islamic year (12 months) is 10631 / 30 = 354.36666... days.
If day 0 (zero) is the first day of the above cycle of 30 Islamic years,
then the number of the year to which day N belongs equals
floor ((30N+k)/10631) provided k is between
26 (included) and 27 (excluded).
Such a choice of k ensures that two critical inequalities are satisfied:
For year 16 to be longer than year 15, day 5669 must belong to year 16 and not
15. This requires k to be at least
16*10631-30*5669 = 26.
On the other hand, for year 26 to be longer than year 27, day 9567 must be in year 26 rather
than 27, which implies that k must be strictly less than
27*10631-30*9567 = 27.
These two inequalities are sufficient to satisfy the 60 constraints imposed by
the entire 30-year pattern.
Using k = 26, we obtain a formula (valid for an
indefinite number of 30-year Islamic cycles)
which gives the Islamic year Y corresponding to day N :
Y = floor ( [ 30 N + k ] / 10631 )
Conversely, the number NY corresponding to the first day of Islamic year Y is:
NY = ceiling ( [ 10631 Y - k ] / 30 )
Subtracting this quantity from the original day number (N) we obtain
a number N' from 0 to 354 within the Islamic year.
From this number N', the Islamic month is not difficult to obtain.
Conversely, we may also get the number of the first day of the month.
The number within the month is obtained by subtracting that from N'.
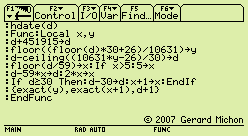
All this can be embodied into two computer routines which convert a day number
to an Islamic date (hdate) and vice-versa (hday).
For compatibility with the similar routines
for the Gregorian and Julian calendars, we count days from the MJDN origin,
with an offset of 451915 days.
The following implementations are for the TI-92,
TI-89 and Voyage 200
handheld calculators.
 |
|
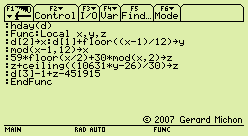 |
hday({y2,m2,d2}) - hday({y1,m1,d1}) is
the number of days between two Hijri dates.
hdate ( hday ( {yyyy,mm,dd} )) puts a
"
generalized" Hijri date in standard form.
date ( hday ( {yyyy,mm,dd} )) obtains a Gregorian date from a Hijri date.
hdate (
day ( {yyyy,mm,dd} )) obtains a Hijri date from a Gregorian one.
Competing
Variants of the Tabular Islamic Calendar :
The aforementioned date of
Friday July 16, 622 CE
is by far the most common starting point of the Hegira calendar,
but it may also be reckoned from Thursday
July 15, 622 CE.
This so-called "Thursday" calendar would be obtained with an offset
of 451916 days (instead of 451915) in both of the above routines.
There are no fewer than 30 regular
intercalatory patterns which would be based
on the same 30-year period (of 10631 days) as above.
Apparently, only four of those have ever been advocated
(as tabulated below).
The four extant intercalatory patterns agree that years 2, 5, 13, 21 and 24
(modulo 30) are "long" years of 355 days,
but disagree on some of the remaining 6 long years in the 30-year cycle of 10631 days.
This amounts to different values of k
for the calendrical formulas introduced above
(with k = 26) :
The 8 Extant Variants of the Tabular Islamic Calendar
| Long Years (modulo 30) |
kmin | kmax | Friday | Thursday |
|---|
| 2, 5, 7, 10, 13, 15, 18, 21, 24, 26, 29 |
25 | < 26 | Ic | Ia |
| 2, 5, 7, 10, 13, 16, 18, 21, 24, 26, 29 |
26 | < 27 |
IIc | IIa |
| 2, 5, 8, 10, 13, 16, 19, 21, 24, 27, 29 |
29 | < 30 | IIIc | IIIa |
| 2, 5, 8, 11, 13, 16, 19, 21, 24, 27, 0 |
1 | < 2 | IVc | IVa |
To make the above calendrical functions match your favorite
variation:
- Change the constant 26 (which appears 3 times) into 25, 26, 29 or 1.
- Use 451915 for a Friday calendar, or 451916 for a Thursday calendar.
The above numbering of the 8 extant variants of the Tabular Islamic Calendar follows
the classification given by
Robert Harry van Gent,
who calls "civil" (c) the tabular calendar
based on the usual starting point of July 16, 622 CE
and "astronomical" (a) the "Thursday" calendar based on a July 15 starting point.
| Ic | - Kushyar
ibn Labban (AD 971-1029).
- Ulugh
Beg (AD 1393-1449).
- Convertisseur de date,
Ministère des Habous et des Affaires Islamiques.
- Gregorian-Hijri Dates Converter, by Waleed Muhanna.
|
|---|
| Ia | - Microsoft's
algorithm (misleadingly called the
Kuwaiti algorithm).
- Islam Online's
Date Converter.
- Al-Islam's Agenda-Date Converter
(Ministry of Islamic Affairs, Saudi Arabia).
|
|---|
| IIc | - Gnu Emacs editor (courtesy of Dershowitz and Reingold).
- Calendrica,
by Edward M. Reingold and Nachum Dershowitz.
- Numericana, by Gérard P. Michon.
- Calendar Magic, by Alex Balfour.
- Today's Date, by Doug Zongker.
- Java Calendar Conversions, by Mark E. Shoulson.
- Fourmilab's Calendar Converter,
by John Walker.
- Conversion of Islamic and
Christian dates, by Johannes Thomann.
- Muslim Holidays.
Dates of Religious and Civil Holidays Around the World.
- Hijri/Gregorian/Julian
Converter, by Tarek Maani.
- The Islamic Calendar,
by Claus Tøndering.
|
|---|
| IIIa | - Fatimid Calendar. Misri calendar. Bohra calendar.
- Date Exchange, by Sualeh Fatehi.
- Hijri Calendar
(Dawoodi Bohra Version).
|
|---|
| IVa | - Ahmad ibn 'Abdallah Habash al-Hasib
al-Marwazi (d. ca. AD 870).
- Abu Arrayhan Muhammad ibn Ahmad
al-Biruni
(AD 973-1048).
- Elias of Nisibis or Elias bar Senaya, Patriarch
Elias I
of Tirhan (1028-1049).
|
|---|
Many of the above authors do point out that such arithmetic approximations
are not a substitute for the actual
observational Islamic calendar
sanctioned by religious authorities.
Reingold and Dershowitz
(
Calendrica)
also provide an "observational" [sic] Islamic calendar, based on more precise astronomical
computations to better predict the religious beginning of each Islamic month.

